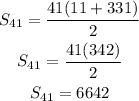Input data
11, 19, 27
An arithmetic sequence is a sequence in which the difference between each consecutive term is constant. An arithmetic sequence can be defined by an explicit formula in which an = d (n - 1) + c, where d is the common difference between consecutive terms, and c = a1.
Procedure
d = 19 - 11 = 8
d = 27 - 19 = 8
a1 = 11
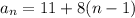
for n = 41
To find the sum of the first n terms of an arithmetic series use the formula, n terms of an arithmetic sequence use the formula,

a41 = 11+8(41-1)
a41 = 11+8*40
a1 = 331