Question

Quadnlateral ABCD is graphed on the set of axes below. When ABCD is rotated 90 in a counterclockwise direction about the origin, its image is quadrilateral A'B'C'D' Is distance preserved under this rotation, and whuch coordinates are correct for the given vertex"? 1) no and C (1,2) 2) no and D' (24) 3) yes and A'(6,2) 4) yes and B'(-24) Option 1 Option 2 Option 3

Answer 1

The rotation operation preserves the distance of the figure. We just change its orientation but the distance stays the same.

Rotation about 90 degrees will change the coordinates of the quadrilateral via the equation

`R_((0,0),90)(x,y)=(-y,x)`

Hence, for the vertices of the given quadrilateral on the figure, the following will be the new vertices upon rotation of the quadrilateral about 90 degrees counterclockwise.

`\begin{gathered} A(-2,6)\rightarrow\rightarrow A^(\prime)(-6,-2) \\ B(4,3)\rightarrow\rightarrow B^(\prime)(-3,4) \\ C(2,-1)\rightarrow\rightarrow C^(\prime)(1,2) \\ D(-4,2)\rightarrow\rightarrow D^(\prime)(-2,-4) \end{gathered}`

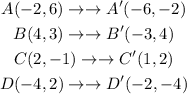
Based on the provided solution above, the answer to this problem would be yes and B'(-3,4), which is option 4.

Answer: Option 4