Question

Sketch a graph of the relation. Is the relation a function?

Answer 1

A.

The domain of a function is the complete set of possible values of the independent variable:

`\begin{gathered} _{\text{ }}Domain\colon\mleft\lbrace-5,1,3\mright\rbrace \\ \end{gathered}`

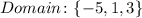
The range of a function is the complete set of possible values of the dependent variable:

`_{\text{ }}Range\colon\mleft\lbrace-4,-2,0,2,4\mright\rbrace`

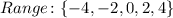
A function is a specific type of relation in which each input value has one and only one output value.

Since:

(-5,4) and (-5,4) and (1,2) and (1,-2) belong to the relation. We can conclude that the relation is not a function.

B.

`\begin{gathered} _{\text{ }}Domain\colon\mleft\lbrace-3,-1,0,1,3\mright\rbrace \\ _{\text{ }}Range\colon\mleft\lbrace-1,1,6\mright\rbrace \end{gathered}`

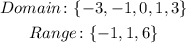
Since:

`\begin{gathered} x1\\e x2\\e x3\\e x4\\e x5 \\ -3\\e-1\\e0\\e1\\e3 \end{gathered}`

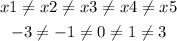
We can conclude that the relation is a function