To find the equation in slope-intercept form, we shall begin by finding the slope of the line.
First step is to identify two different points on the line. Observe carefully that when x equals 0, y equals 2. Therefore we have (0, 2). Also when x equals 2, y equals negative 6. Therefore, the other point is (2, -6). With these two points we can now calculate the slope as follows;
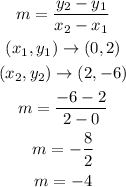
With the slope derived as -4, we can now determine the value of b (the y-intercept). We shall take any of the points above, hence let use the first point;

The equation therefore is y = -4x + 2