Question

To figure out how many vacation days she had left to use, Mona looked overher old calendars to figure out how many days of vacation she had taken eachyear.Vacation days taken by MonaYear Vacation days20098201016201125201213201326According to the table, what was the rate of change between 2010 and 2011?vacation days per year

Answer 1

We are asked to determine the rate of change of the values of vacation days between 2010 and 2011.

To do that we will use the following formula:

`r=(f(t_2)-f(t_1))/(t_2-t_1)`

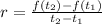
Where:

`\begin{gathered} f(t_2),f(t_1)=\text{ vacation days for t2 and t1 respectively} \\ t_2,t_1=\text{ years in cosideration. } \end{gathered}`

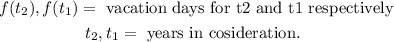
For the given case we have:

`\begin{gathered} t_2=2011 \\ t_1=2010 \end{gathered}`

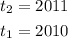
The vacation days associated to each of the years are:

`\begin{gathered} f(2010)=16 \\ f(2011)=25 \end{gathered}`

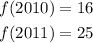
Now, we plug in the values in the formula for rate of change:

`r=(25-16)/(2011-2010)`

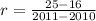
Now, we solve the operations:

`r=(9)/(1)=9`

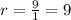
Therefore, the rate of change is 9 days per year.