Question

I need help with this practice problem solvingI will send an additional pic that is the answer options for this problem

Answer 1

The parametric equations of a function are:

x = 4 cos θ

y = 3 sin θ

For angles in the interval:

`\lbrack(\pi)/(2),(3\pi)/(2)\rbrack`

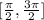
Below we show the table of values for theta in increments of 10 degrees and the corresponding values of x and y:

This produces the following graph:

The graph was drawn from the upper points down to the left-bottom points, that is, in a counterclockwise direction.

The ellipse is centered at the origin and the length of the major axis is 4 and the length of the minor axis is 3.

Completing the full statement:

The graph of the parametric equations is the left half of an ellipse. The length of the major axis of the semi-ellipse is 4, the length of the minor axis is 3, and the center is the origin. The semi-ellipse is elongated horizontally.

Arrows are drawn on the semi-ellipse to indicate movement in a counterclockwise direction.