the sum of internal angles of a 4-sides figure is 360° ever then
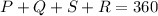
we know P and R is a right angles then is 90°, then we can replace
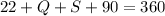
simplify
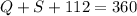
and the angles Q and S are the same because the kite is symmetrical then Q=S
and we can replace Q=S
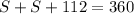
simplify
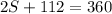
and solve for S
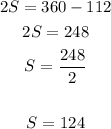
then right option is D 124