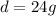Question

I need help with the equation (sorry for the lines)

Answer 1

Given the ordered pairs in the table, we would have the y values as the distance d, and x values as the gas in gallons g.

This means for every value of x, there is a corresponding value of y.

Note also that the d values (or y values) has a 24 unit increment at every point while, the g values (x values) has 1 unit increment for every point. We can write an equation for this by first calculating the slope, that is, rate of change as follows;

`m=(y_2-y_1)/(x_2-x_1)`

The variables here would be;

`\begin{gathered} (x_1,y_1)=(5,120) \\ (x_2,y_2)=(6,144)_{} \end{gathered}`

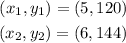
The slope therefore is;

`\begin{gathered} m=(144-120)/(6-5) \\ m=(24)/(1) \\ m=24 \end{gathered}`

Using the general form of the equation in slope-intercept form, we would have

`\begin{gathered} y=mx+b \\ \text{Where:}(x,y)=(5,120) \\ 120=24(5)+b \\ 120=120+b \\ \text{Subtract 120 from both sides;} \\ b=0 \end{gathered}`

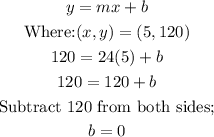
We can now write out the equation for this relationship as follows;

`\begin{gathered} y=mx+b \\ y=24x+b \\ \text{Where b}=0 \\ y=24x+0 \\ y=24x \end{gathered}`

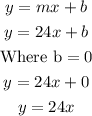
Note here that the variables as provided in the question are d and g. we can substitute these and re-write our equation as;

ANSWER:

`d=24g`