For any given triangle. The sum of two sides must be greater than the length of the third side.
This means, with two sides given as 20 inches and 12 inches (1 foot = 12 inches), we can conclude that;
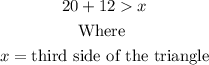
From this inequality we can now deduce the following;
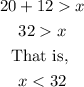
Alo, we have;
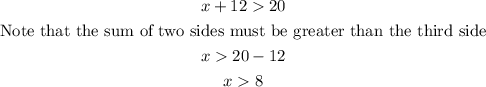
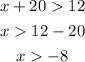
The length of the third side cannot be a negative number, hence we shall disregard the third option, that is x > -8.
Therefore, the possible length for the third side shall be
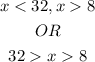
The possible length of the third side shall be either
Less than 32 inches
OR
Greater than 8 inches