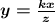Question

Y varies directly as x and inversely as z can be modeled by the equation ______

Answer 1

Direct variation is a relationship between two variables. In this case, y is directly proportional to x. We say y varies directly with x if:

`\begin{gathered} y=kx \\ \text{ Where k is a constant} \end{gathered}`

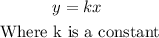
On the other hand, inverse variation is another relationship between two variables. In this case, y is inversely proportional to x. We say y varies inversely with x if:

`y=(k)/(x)`

Now, if we combine the two previous definitions, we have:

`\begin{gathered} y=kx\Rightarrow\text{ Because y varies directly with x} \\ y=(kx)/(z)\Rightarrow\text{ Because y varies inversely with z} \end{gathered}`

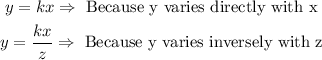
Therefore, y varies directly as x and inversely as z can be modeled by the equation

`$$\boldsymbol{y=(kx)/(z)}$$`