Use the following formula:
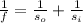
where,
f: focal length of the mirror = 1.5 cm (positive because it is concave)
so: object distance = 3.0cm
si: image distance = ?
Solve the equation above for si:
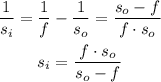
Then, replace the values of the given parameters and simplify:
![s_i=\frac{(1.5cm)(3.0cm)}{3.0\operatorname{cm}-1.5\operatorname{cm}}=\frac{4.5\operatorname{cm}^2}{1.5\operatorname{cm}}=3.0\operatorname{cm}]()
Hence, the image distance is 3.0cm