Question

Four functions are given below. Either the function is defined explicitly, or the entire graph of the function is shown.For each, decide whether it is an even function, an odd function, or neither.

Answer 1

Summary of even and odd functions

A function f is even if the graph of f is symmetric with respect to the y-axis. Algebraically, f is even if and only if f(-x) = f(x) for all x in the domain of f.

A function f is odd if the graph of f is symmetric with respect to the origin. Algebraically, f is odd if and only if f(-x) = -f(x) for all x in the domain of f.

From the definition itself, we see how can we test if the functions are even or odd.

- First graph (to the left)

From the graph, we see that the function is symmetric with respect to the y-axis because the left side (x<0) is a reflection (along the y-axis) of the right side (x>0), so it is an even function.

- Second graph (to the right)

From the graph, we see that the function is symmetric with respect to the origin, the left side (x<0) is a reflection (along with the origin) of the side to the right (x>0), so it is an odd function.

- First function (to the left)

The function:

`g(x)=5x^2`

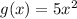
is an even function because we see that:

`g(-x)=5\cdot(-x)^2=5x^2=g(x)`

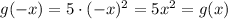
- Second function (to the right)

The function:

`h(x)=-2x^5+3x^3`

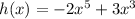
is an odd function because we see that:

`h(-x)=-2\cdot(-x)^5+3\cdot(-x)^3=-(-2x^5+3x^3)=-h(x)^{}`

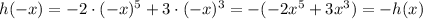
Summary

We have the following results:

- First function (to the left): even

- Second graph (to the right): odd

- First function (to the left): even

- Second function (to the right): odd