Question

Find A. Measure of angle AB. Measure arc CEC. Measure of angle CD. Measure of angle DE. Measure of angle ABE

Answer 1

Step-by-step explanation

A chord is a segment that links two points from a circumference. When two chords share an extreme they form an angle in that point and an arc with their remaining extremes. The angle is known as an inscribed angle and the arc is its intercepted arc. For any inscribed angle in a circle its measure is the half of the measure of its intercepted arc. As you can see angle A is formed by the chords AB and AD which means that arc BD is its intercepted arc. Then the measure of A is given by:

`\begin{gathered} \angle A=(1)/(2)\measuredangle BD=(1)/(2)78^(\circ) \\ \angle A=39^(\circ) \end{gathered}`

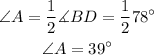
Then we have to find the measure of arc CE. It's the intercepted arc of angle EBC which has a measure of 20°. Then the measure of arc CE is the double of this quantity:

`\measuredangle CE=2\angle EBC=2\cdot20^(\circ)=40^(\circ)`

Angle C is the inscribed angle of the arc BD just like angle A which means that the measure of C is the same that the measure of A. Then we get:

`\angle C=\angle A=39^(\circ)`

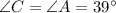
The angle D has arc AC as its intercepted arc so its measure is given by:

`\angle D=(1)/(2)\measuredangle AC=(1)/(2)84^(\circ)=42^(\circ)`

Arc AC is also the inscribed arc of angle ABC which means that the measure of this angle is the same as the measure of D:

`\angle ABC=\angle D=42^(\circ)`

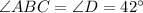
Angle ABE is given by the sum of angle ABC and angle B so its measure is:

`\angle ABE=\angle ABC+\angle B=42^(\circ)+20^(\circ)=62^(\circ)`

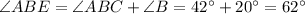
Answers

A. 39°

B. 40°

C. 39°

D. 42°

E. 62°