Question

A balloon artist counted the number of balloon animal requests he received at a party. The balloon equests differed in animal type and color. Giraffe Dog Purple 8 9 Green 5 6 Yellow 9 3 Vhat is the probability that a randomly selected balloon animal is yellow or is shaped like a giraffe? Simplify any fractions.

Answer 1

The probability that a randomly selected balloon animal is yellow or is shaped like a giraffe is given by

`P(yellow\: or\: giraffe)=P(yellow)+P(giraffe)-P(yellow\: and\: giraffe)`

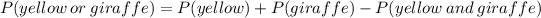
Let us first find the probability that a randomly selected balloon animal is yellow

`P(yellow)=\frac{n(\text{yellow)}}{n(\text{total)}}`

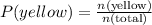
Where n(yellow) is the total of the row yellow

`n(yellow)=9+3=12`

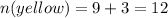
n(total) is the total number of balloon animals

`n(total)=8+9+5+6+9+3=40`

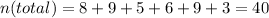
So, the probability that a randomly selected balloon animal is yellow is

`P(yellow)=\frac{n(\text{yellow)}}{n(\text{total)}}=(12)/(40)=(3)/(10)`

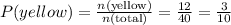
Now, let us find the probability that a randomly selected balloon animal is shaped like a giraffe

`P(giraffe)=\frac{n(giraffe\text{)}}{n(\text{total)}}`

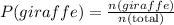
Where n(giraffe) is the total of the column giraffe

`n(giraffe\text{)}=8+5+9=22`

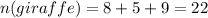
So, the probability that a randomly selected balloon animal is shaped like a giraffe is

`P(giraffe)=\frac{n(giraffe\text{)}}{n(\text{total)}}=(22)/(40)=(11)/(20)`

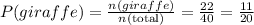
Now, let us find the probability that a randomly selected balloon animal is yellow and shaped like a giraffe

`P(yellow\: and\: giraffe)=\frac{n(yellow\: and\: giraffe)}{n(\text{total)}}`

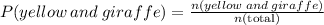
Where n(yellow and giraffe) is 9 (the intersection of yellow and giraffe)

`P(yellow\: and\: giraffe)=\frac{n(yellow\: and\: giraffe)}{n(\text{total)}}=(9)/(40)`

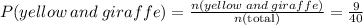
Finally, the probability that a randomly selected balloon animal is yellow or is shaped like a giraffe is

`\begin{gathered} P(yellow\: or\: giraffe)=P(yellow)+P(giraffe)-P(yellow\: and\: giraffe) \\ P(yellow\: or\: giraffe)=(3)/(10)+(11)/(20)-(9)/(40) \\ P(yellow\: or\: giraffe)=(5)/(8) \end{gathered}`

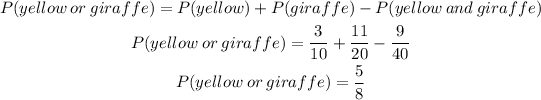
Therefore, the probability that a randomly selected balloon animal is yellow or is shaped like a giraffe is 5/8