Question

A farmer has a 25 ft by 100 ft rectangular field that he wants to reduce to 16% of its original size. How wideof a strip should he cut around the edge of his field to do this?

Answer 1

10feet

Given:

A farmer has a 25 ft by 100 ft rectangular field that he wants to reduce to 16% of its original size.

To find how wideof a strip he can cut around the edge of his field to do this.

Let w be the width of a strip should he cut around the edge to reduce to 16%

Original area = 25 x 100 = 2500 ft²

Hence;

(25 - 2w)(100 - 2w)= 16% of 2500

(25 - 2w)(100 - 2w) = 0.16 x 2500

(25 - 2w)(100 - 2w) =400

Open the parenthesis.

2500 - 50w - 200w + 4w² = 400

Rearrange in the form of quadratic equation.

2500 - 250w + 4w² - 400 = 0

2100 - 250 w + 4w² = 0

4w² - 250w + 2100 = 0

Divide through by 2

2w² - 125w + 1050 = 0

We can now solve the above using using the quadratic formula.

a = 2 b=-125 c=1050

`w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

`w=\frac{125\pm\sqrt[]{15625-8400}}{4}`
`=\frac{125\pm\sqrt[]{7225}}{4}`
`=(125\pm85)/(4)`

`\begin{gathered} \text{Either } \\ w=(125+85)/(4)=(210)/(4)=52.5 \\ \\ or \\ \\ w=(125-85)/(4)=(40)/(4)=10 \end{gathered}`

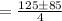
Let's check for the reasonable solution.

(25 - 2w)(100 - 2w) = 400

w=10

(25 - 20)(100 - 20) = (5)(80) = 400

The only reasonable solution is w= 10

Therefore, the widthof the strip should be 10 feet.