Question

The engine of a large ship does 1.85 ✕ 108 J of work with an efficiency of 4.00%. (a) How much heat transfer (in J) occurs to the environment? (b) How many barrels of fuel are consumed, if each barrel produces 6.00 ✕ 109 J of heat transfer when burned?

Answer 1

• Given:

Work done = 1.85 x 10⁸ J

Efficiency = 4%

Let's solve for the following:

• (a). How much heat transfer (in J) occurs to the environment?

Apply the formula:

`\eta=(W)/(Q_h)`

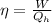
Where Qh is the amount of heat transfer.

rewrite the formula for Qh:

`Q_h=(W)/(\eta)`

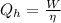
The equation for the work done by the engine will be:

`W=Q_h-Q_c`

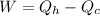
Now, substitute W/n for Wh in the equation for the work done:

`\begin{gathered} W=(W)/(\eta)-Q_c \\ \text{ } \\ Rewrite\text{ the equation for }Q_c: \\ Q_c=(W)/(\eta)-W \\ \\ Q_c=W((1)/(\eta)-1) \end{gathered}`

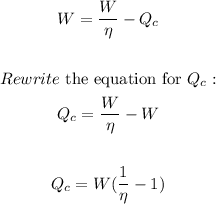
Where:

n is the efficiency = 4% = 0.04

W is the work done.

Plug in the values and solve for Qc:

`\begin{gathered} Q_c=(1.85*10^8)((1)/(0.04)-1) \\ \\ Q_c=(1.85*10^8)(25-1) \\ \\ Q_c=(1.85*10^8)(24) \\ \\ Q_c=4.44*10^9\text{ J} \end{gathered}`

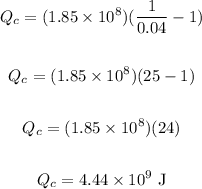
Therefore, the amount of heat transfer that occurs in the environment is 4.44 x 10⁹ J.

• Part B:

Given:

Amount of heat produced by each barrel when burned = 6.00 x 10⁹ J.

To find the amount of barrels of fuel consumed, apply the formula:

`N=(Q_c+W)/(6.00*10^9)`

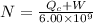
Substitute values in the formula and solve for N, where N is the number of barrels of fuel burned.

`\begin{gathered} N=((4.44*10^9)+(1.85*10^8))/(6.00*10^9) \\ \\ N=0.771 \end{gathered}`

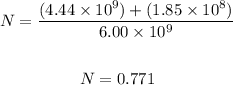
Therefore, the amount of fuel consumed is 0.771 barrels.

ANSWER:

• (a). 4.44 x 10⁹ J

• (b). 0.771 barrels.