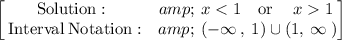Question

Pleas help me find the composition of goh and it’s domain

Answer 1

The function is given below as

`\begin{gathered} g(x)=(x+4)/(x-1) \\ h(x)=2x-1 \end{gathered}`

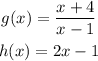
To figure out

`(goh)(x)`

To do this , we will substitute x= 2x-1 in g(x)

`\begin{gathered} g(x)=(x+4)/(x-1) \\ g(h)(x)=(2x-1+4)/(2x-1-1) \\ g(h)(x)=(2x+3)/(2x-2) \end{gathered}`

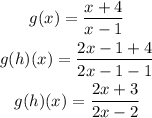
Hence,

The composte function will be

`(goh)(x)=(2x+3)/(2x-2)`

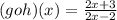
Step 2:

To figure out the domain,

In mathematics, the domain of a function is the set of inputs accepted by the function.

Hence,

The domain of the function is

`\begin{bmatrix}\mathrm{Solution:}\:&\:x<1\quad \mathrm{or}\quad \:x>1\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:1\right)\cup \left(1,\:\infty \:\right)\end{bmatrix}`