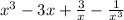The given expression is
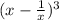
According to Pascal's Triangle, the third row is 1 3 3 1.
This means the binomial expansions must have 4 terms, where each number belongs to each of them as a coefficient.
Now, the binomial expansion would be

Now, we need to solve each parenthesis using the distributive property.
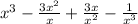
Then, we simplify variables, remember that division of powers is solved by subtracting exponents
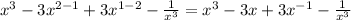
At last, we place the negative power as denominator