Question

It is estimated that about 7,217 African cheetahs are living in the wild today and thepopulation is expected to decline at a rate of 8.4% per year. Predict the number ofAfrican cheetahs living in the wild in 23 years. Round answer to a whole number.

Answer 1

Answer: 959

Step-by-step explanation:

Step 1. The information that we have is:

The initial or actual amount of African cheetahs is 7,217, we will call this 'a':

`a=7,217`

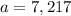
The rate of decline for the population is 8.4% per year, this will be 'r':

`r=8.4`

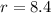
Converting this amount from percentage to decimal number:

`\begin{gathered} r=8.4/100 \\ r=0.084 \end{gathered}`

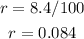
And we require to find the number of cheetahs in 23 years, this will be the time 't':

`t=23`

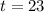
Step 2. This problem is an example of exponential decay, and the formula to use is:

`y=a(1-r)^t`

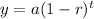
Where 'y' represents the final amount after time t.

Step 3. Substituting the known values:

`y=7,217(1-0.084)^(23)`

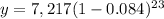
Step 4. Solving the operations:

`y=7,217(0.916)^(23)`
`y=7,217(0.132921702)`

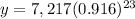
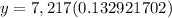
The result is:

`y=959.296`

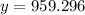
Rounding this result to the nearest whole number:

`y=959`

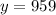
The prediction is 959 African cheetahs.

Answer: 959