Question

Parallelogram can be represented by [5/2 -5/3]. what is it’s area?

Answer 1

We are given that a parallelogram can be represented by the following matrix:

`\begin{bmatrix}{5} & {-5} \\ {2} & {3}\end{bmatrix}`

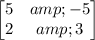
The area of a parallelogram represented by a 2x2 matrix is the determinant of the matrix. The determinant of a matrix of the form:

`\begin{bmatrix}{a} & {b} \\ {c} & {d}\end{bmatrix}`

Is given by:

`det(\begin{bmatrix}{a} & {b} \\ {c} & {d}\end{bmatrix})=ad-bc`

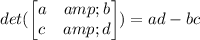
Therefore, the determinant is:

`det(\begin{bmatrix}{5} & {-5} \\ {2} & {3}\end{bmatrix})=(5)(3)-(-5)(2)=15+10=25`

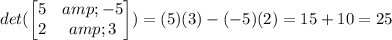
Therefore, the area of the parallelogram is 25 square units.