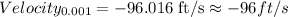EXPLANATION
Given that the arrow function is as follows:
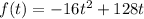
The instantaneous velocity is given by the following relationship:
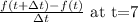
For △t = 0.1:
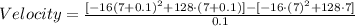
Computing the powers:
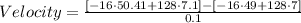
Multiplying numbers:
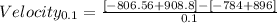
Removing the parentheses and adding numbers:
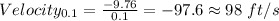
For △t=0.01
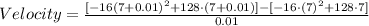
Computing the powers:
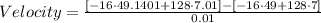
Multiplying numbers:
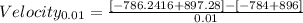
Adding numbers:
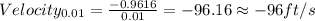
For △t = 0.001
Applying the same reasoning than before, give us the following result: