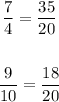We have the fraction
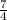
We want to rewrite it as
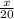
Where x is a number that we don't know, but it will turn the fraction equivalent, then we can say that
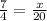
We can do a cross multiplication and solve it for x
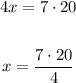
Then in fact, to discover the new numerator we must do
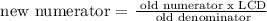
Let's do it then!
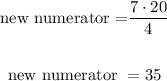
Then
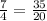
The equivalent fraction is 35/20
Now for the second question, we can use the logic

The equivalent fraction is
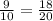
Final answers: