Question

one gram of water becomes 1671cm³ of steam when boiled at a pressure of one atmospheric. if the specific latent heat of vaporization of water is 2260 kJ/kg. Calculate (a) the external work done (b) the increase in external energy

Answer 1

We need to calculate the work done and the increase in external energy. The external work can be calculated as:

`W=P\Delta V`

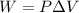
where P is the pressure and delta V denotes the change in volume.

The increase en external energy is given by:

`\Delta E=Q-W`

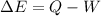
where W is the work done by external forces and Q is the heat transfer.

Before we begin we convert the units to the correct units:

`\begin{gathered} m=0.001kg \\ V_1=1*10^(-6)m \\ V_2=1671*10^(-6)m \\ P=101325\text{ Pa} \end{gathered}`

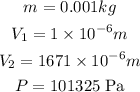
a)

Plugging the values we know we have that:

`\begin{gathered} W=101325(1671*10^(-6)-1*10^(-6)) \\ W=169.21 \end{gathered}`

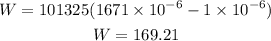
Therefore, the work done is 169.21 J

b)

The heat transfer is given by:

`Q=mL`

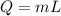
then we have:

`\begin{gathered} Q=(0.001)(2260*10^3) \\ Q=2260 \end{gathered}`

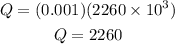
Once we know this we have that the change in external energy is:

`\begin{gathered} \Delta E=2260-169.21 \\ \Delta E=2090.79 \end{gathered}`

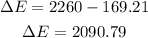
Therefore, the increase in external energy is 2090.79 J