What is the percent composition of carbon dioxide within the gaseous mixture?Please select either A,B,C, or D at the end.

Question

asked Jan 2, 2023 144k views

1 Answer

Yalian · Answer 1 · 2023-01-08T09:05:26+0000

The percent composition of a compound is its mass percent with respect to the sample total mass.

We already know tha sample mass, 200.0 g, to find the mass of the carbon dioxide, CO₂, we can use its molar mass and the measured number of moles:

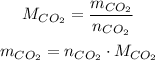
$\begin{gathered} M_{CO_(2)}=\frac{m_(CO_2)}{n_{CO_(2)}}_{} \\ m_(CO_2)=n_(CO_2)\cdot M_{CO_(2)} \end{gathered}$

We know that the molar mass is 44.01 g/mol, and the number of moles is 0.30 mol, so:

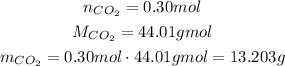
$\begin{gathered} n_{CO_(2)}=0.30mol_{} \\ M_{CO_(2)}=44.01g\/mol \\ m_(CO_2)=0.30mol\cdot44.01g\/mol=13.203g \end{gathered}$

Now, we check the percent of 13.203g with respect to the total 200.0 g:

200.0g ---- 100%

13.203g ---- P

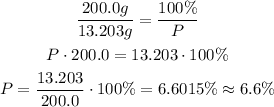
$\begin{gathered} (200.0g)/(13.203g)=(100\%)/(P) \\ P\cdot200.0=13.203\cdot100\% \\ P=(13.203)/(200.0)\cdot100\%=6.6015\%\approx6.6\% \end{gathered}$

By comparison, we can see that this corresponds to alternative D.