Question

Christine tracked her calorie intake for a week. Determine what the standard deviation is from thedata below.

Answer 1

We will determine the standard deviation as follows:

*First we have to remember the expression:

`\sigma=\sqrt[]{(1)/(N)\sum ^N_(i=1)(x_i-\mu)^2}`

Now, we determine the count (N), this is N = 7 [Since there are 7 vvalues on the dataset].

Second: We calculate the sum:

`\sum ^7_(i=1)(x_i-\mu)^2`

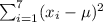
Bu for this, we will determine the mean (miu), and:

`\mu=2092.8571428571`

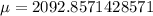
Thus:

`.`
`\sigma=\sqrt[]{8163.2653061224}\Rightarrow\sigma=90.350790290525`

So, the standard deviation is aproximately 90.