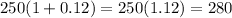Question

Jenna weighed 250 pounds in August but weighed 280 pounds by December. What is the percent increase in her weight? ANS. _________. %

Answer 1

As Jenna weighed 250 pounds in August, this will represent 100%

`\begin{gathered} 250lb\rightarrow100percent \\ 280lb\rightarrow xpercent \end{gathered}`

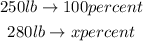
This relation leads to the next equation

`\begin{gathered} x_{\text{percent}}=\frac{280lb\cdot100_{\text{percent}}}{250lb} \\ \Rightarrow x_{\text{percent}}=\frac{28000_{\text{percent}}}{250} \\ \Rightarrow x_{\text{percent}}=112_{\text{percent}} \end{gathered}`

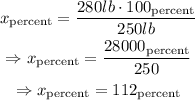
Therefore, the increment in weight is given by

`x_{\text{percent}}-100=12_{\text{percent}}`

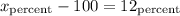
So, the percent increase is 12%

A way of making sure our answer is correct is by doing the next operation

`250(1+0.12)=250(1.12)=280`