Given:
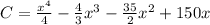
Let's solve for the following:
• (a). Find C'(x).
Here, we are to find the derivative of C(x).
Apply the sum rule:
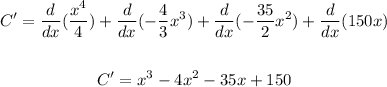
• (b). The critical numbers of C(x).
The critical numbers will be the points where the graph changes direction.
Using the derivative, let's solve for x.
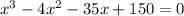
Factor the left side using the rational root test:
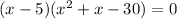
Now factor using the AC method:
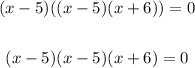
Equate each factor to zero and solve for x:
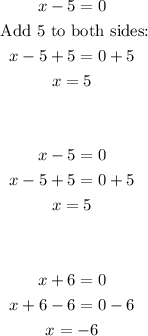
Therefore, the critical numbers of C(x) are:
x = -6, 5
• (C). Increasing interval.
Use the critical points to find the increasing and decreasing intervals.
Using interval notation, the increasing interval is:
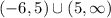
• D. Decreasing interval:
Using interval notation, the decreasing interval is:
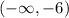
ANSWER:
(a). C'(x) = x³ - 4x² - 35x + 150
(b). x = -6, 5
(c). Increasing: (-6, 5) U (5,∞)
Decreasing: (-∞, -6)