We have to calculate the electric field in the center, so we need the distance to the center R and the interaction of each charge with that point
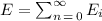
To calculate the distance R we have a triangle
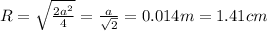
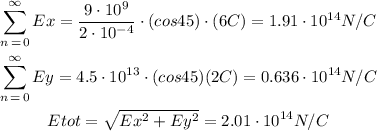
Is important to remember that E has direction so you have to calculate each axis, x, and y