Question

The nutty professor sells cashews for $6.20 per pound and Brazil nuts for $4.30 per pound. How much of each type should be used to make a 32 pound mixture that sells for $5.37 per pound?

Answer 1

Let's call C the weight of the Cashews and B the weight of the Brazil nuts.

Since the professor wants to sel a 32 pound mixture, we have the following equation:

`C+B=32.`

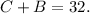
Now, since the price of the mixture will be $5.37 per pound, this means the price of the whole mixture will be

`32\cdot5.37=171.84.`

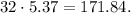
This leads us to the followin equation:

`6.20C+4.30B=171.84.`

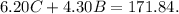
Now we have a system of equations:

`C+B=32`
`6.20C+4.30B=171.84.`

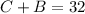
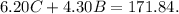
To solve it, let's isolate one of the variables in the first equation by subtracting B from both sides of it:

`C=32-B\text{.}`

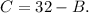
Now, let's use this value of C in the second equation:

`6.20(32-B)+4.30B=171.84,`
`198.4-6.20B+4.30B=171.84,`
`198.4-1.9B=171.84.`

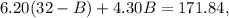
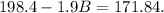
To solve this equation, let's subtract 198.4 from both sides of it:

`-1.9B=-26.56.`

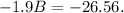
Then, let's divide both sides by -1.9:

`B\approx13.98.`

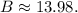
Using this value of B in the first equation will give us:

`C=32-13.98=18.02.`

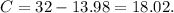
These would be the values of B and C round to two decimals. If we want, we can also write them as integer numbers. so the mix would need to have 18 pounds of cashews and 14 pounds of Brazil nuts.