Question

(Solve the problem down below & simplify the answer. Round to the nearest hundredth as needed.)

Answer 1

From the given information, we know that the decreasing function values is

`V(t)=3600(3^(-0.15t))`

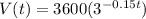
and we need to find the time t when V(t) is equal to $1200. Then by substituting this values into the function, we have

`1200=3600(3^(-0.15t))`

By dividing both sides by 3600, we get

`3^(-0.15t)=(1200)/(3600)=(1)/(3)`

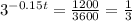
So we have the equations

`3^(-0.15t)=(1)/(3)`

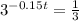
From the exponents properties, we know that

`3^(-0.15t)=(1)/(3^(0.15t))`

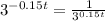
so we have

`(1)/(3^(0.15t))=(1)/(3)`

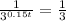
or equivalently,

`3^(0.15t)=3`

This means that

`0.15t=1`

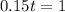
Then, by dividing both sides by 0.15, we obtain

`t=(1)/(0.15)=6.6666`

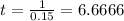
So, by rounding to the nearest hundreadth, the answer is 6.67 years