Question

A steel railroad track has a length of 24 mwhen the temperature is 8°C.What is the increase in the length of therail on a hot day when the temperature is36 °C? The linear expansion coefficient ofsteel is 11 x 10-6(°C)-1.Answer in units of m.Answer in units of mSecond part:- Suppose the end of rail are rigidly clamped eight Celsius degrees to prevent expansion calculate the thermal stress in the rail if it’s temperature is raised to 36 Celsius degrees Young’s module for Steel is 20×10 to the power of 10 and N/m to the power of two answer in units of N/m to the power of two.

Answer 1

Given:

• Length = 24 m

,

• Temperature, T1 = 8°C

,

• Expansion coefficient = 11 x 10⁻⁶(°C)⁻¹

Let's solve for the following:

• (a). The increase in length of the rail when the temperature is 36 °C

To find the increase in length, apply the formula:

`L=L_o*\alpha *(T_2-T_1)`

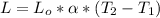
Where:

Lo = 24 m

α = 11 x 10⁻⁶(°C)⁻¹

T2 = 36 °C

T1 = 8°C

Thus, we have:

`\begin{gathered} dL=24*11*10^(-6)*(36-8) \\ \\ dL=24*11*10^(-6)*(28) \\ \\ dL=0.0074\text{ m} \end{gathered}`

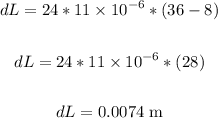
The increase in length is 0.0074 m.

• (b). Let's calculate the thermal stress.

To find the thermal stress, we have the formula:

`\text{ thermal stress = }Y(dL)/(L)`

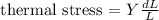
Where:

Y is the young modulus = 20 x 10¹⁰ N/m

dL is the change in length = 0.0074 m

L is the length = 24 m

Input values in the formula and solve:

`\begin{gathered} \text{ thermal stress = 20}*10^(10)*(0.0074)/(24) \\ \\ \text{ thermal stress = 6.17}*10^7\text{ N/m}^2 \end{gathered}`

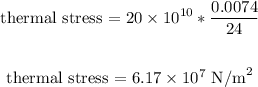
The thermal stress is 6.17 x 10⁷ N/m².

ANSWER:

• (a). 0.0074 m.

• (b). 6.17 x 10⁷ N/m²