SOLUTION:
Case: System of equation word problem
Required: Find the number of adults and children tickets Josie bought.
First we create a system of equation. One for the total number of tickets, the other for the total cost of tickets.
Assumption: Let the number of adult tickets be a and the number of children tickets c.
Sytems of equations:
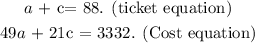
Solving the system of equation, using substitution method

Next we find the value of c
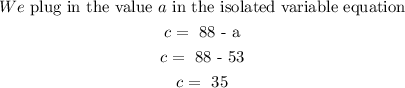
Final answers:
The total number of children tickets bought were 35 WHILE
The total number of adult tickets bought were 53.