Question

Ingrid hit a golf ball. the height of the golf ball (in meters above the ground) t seconds after being hit is modeled by h(t)=-5t²+30tIngrid wants to know when the ball reached its highest point 1) rewrite the function in a different form (factored or vertex) where the awnser appears as a number in the equationh(t)=___2) How many seconds after being hit does the ball reach its highest point?____ seconds

Answer 1

Write the equation in vertex form to find the maximum height, as well as the time when the maximum height is reached.

The vertex form of a quadratic equation is:

`y=a(x-h)+k`

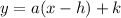
Where (h,k) is the vertex of the parabola, k is the maximum or minimum value and h is the value of x where that maximum or minimum is reached.

To write h in vertex form, complete the square:

`\begin{gathered} h(t)=-5t^2+30t \\ =-5(t^2-6t) \\ =-5(t^2-6t+9-9) \\ =-5((t-3)^2-9) \\ =-5(t-3)^2-5(-9) \\ =-5(t-3)^2+45 \end{gathered}`

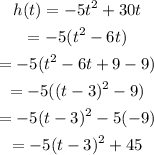
We can see that in this case, the vertex is (3,45).

Therefore:

1)

`h(t)=-5(t-3)^2+45`

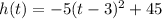
2)

The ball reaches the maximum height 3 seconds after being hit.