Question

What is the area shaded sector to the nearest 10th of the square centimeter?

Answer 1

The area of a sector of a circumference is given by the following formula:

`A=(\theta r^2)/(2)`

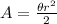
Where r is the radius of the circumference, and θ is the angle of the sector in radians.

The radius is already known: 15cm.

We need to estimate the angle of the shaded region. The shaded region and the sector whose angle is 72° form together a 180° angle. (This is according to the figure. That is not said in an explicit way but we will need to assume that since there is not enough information to calculate the area if it is otherwise.)

Then, the angle of the shaded area, plus 72° is 180°:

`\begin{gathered} \theta+72^o=180^o \\ \\ \theta=180^o-72^o \\ \\ \theta=108^o \end{gathered}`

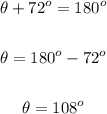
Now, before applying the formula we need to express the angle in radians. Recalling that 180° is equal to π radians:

`\theta=108^o\cdot\frac{\pi\text{ rad}}{180^o}=(108)/(180)\pi\text{ rad}`

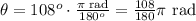
Now, we have the angle in radians. We can use the equation: