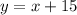Question

Find the equation of a line perpendicular to y +1 = -x that passesthrough the point (-8, 7).

Answer 1

Two lines are perpendicular if the product of their slopes is equal to -1.

Find the slope of the given line. Then, use that result to find the slope of a line perpendicular to it. Use the slope of the line perpendicular to the given line to find the equation of the one that passes through the point (-8,7).

To find the slope of the given line, write it in slope-intercept form by isolating y:

`\begin{gathered} y+1=-x \\ \Rightarrow y=-x-1 \end{gathered}`

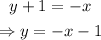
The coefficient of x is -1. Then, the slope of the given line is -1.

Let m be the line perpendicular to y+1=-x.

Since the product of the slopes of perpendicular lines is equal to -1, then:

`\begin{gathered} -1* m=-1 \\ \Rightarrow m=(-1)/(-1) \\ \therefore m=1 \end{gathered}`

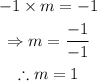
The equation of a line with slope m that passes through the point (a,b) in slope-point form is:

`y=m(x-a)+b`

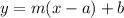
Replace m=1, a=-8 and b=7 to find the equation of the line perpendicular to y+1=-x that passes through the point (-8,7):

`\begin{gathered} y=1(x-(-8))+7 \\ \Rightarrow y=(x+8)+7 \\ \therefore y=x+15 \end{gathered}`

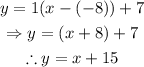
Therefore, the equation of the line perpendicular to y+1=-x that passes through (-8,7) is:

`y=x+15`