Question

What is the arc measure of ct in radians? what is the arc length in feet?

Answer 1

We will determine the arch lenght (In radians) as follows:

*First: We transform the measure of the angle from degrees to radians, that is:

`\theta=80\cdot(\pi)/(180)\Rightarrow\theta=(4\pi)/(9)`

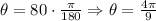
*Second: We find the arc length:

`s=r\theta\Rightarrow s=(13.2)((4\pi)/(9))`
`\Rightarrow s=(88)/(15)\pi`

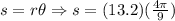
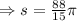
So, the arc length for CT is 88pi/15 radians.

*Third: We find its measure in feet:

`s\approx18.43`

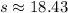
So, the arch length for CT in feet is approximately 18.43 feet.