Question

If an astronaut weighed 200 pounds on the surface of the earth how much would the astronaut weigh 4000 miles above the earths surface. Show working equation

Answer 1

Recall that the gravitational pull is given by

`F=G\frac{m_{}\cdot M_E}{r^2}`

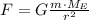
Where m is the mass of the astronaut, ME is the mass of Earth, r is the distance between them, and G is the gravitational constant.

The above relation states that the force of gravitation is directly proportional to the mass of two objects and is inversely proportional to the square of the distance between them.

If the astronaut weighs 200 pounds and the radius of the Earth is 4000 miles then

`\begin{gathered} 200=G(m\cdot M_E)/(4000^2) \\ G\cdot m\cdot M_E=200\cdot4000^2 \end{gathered}`

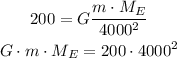
When the astronaut moves 4000 miles above the earth's surface then the distance between them is

4000+4000 = 8000 miles

The distance is measured from the center of the earth so the radius must be included.

So, the new force of gravitation is

`\begin{gathered} F=\frac{G\cdot m_{}\cdot M_E}{r^2} \\ F=(200\cdot4000^2)/(8000^2) \\ F=50\: lb \end{gathered}`

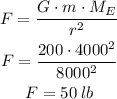
Therefore, the astronaut weighs 50 pounds 4000 miles above the earth's surface.

This makes sense because as you go further away from the center of the Earth then your weight becomes less due to less force of gravity.