Question

A 4.5-m-wide swimming pool is filled to the top. The bottom of the pool becomes completely shaded in the afternoon when the sun is 20° above the horizon.Part AHow deep is the pool?

Answer 1

`4.5\text{ }m`

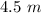
Step-by-step explanation

First, let us make a sketch of the problem:

where r = angle of refraction

d = depth of the pool

First, we have to find the angle of refraction, r, by applying Snell's law:

`(n_1)/(n_2)=(\sin r)/(\sin i)`

where n1 = incident refractive index = 1

n2 = refracted index = 1.33

i = angle of incidence = 70°

Therefore, solving for r, we have that:

`\begin{gathered} (1)/(1.33)=(\sin r)/(\sin70) \\ \\ \sin r=(\sin70)/(1.33)=0.7065 \\ \\ r=\sin^(-1)(0.7065) \\ r=45.0\degree \end{gathered}`

Now, we can solve for the depth of the pool by applying trigonometric ratios for right triangles for tangent:

`\begin{gathered} \tan45=(4.5)/(d) \\ \\ d=(4.5)/(\tan45) \\ \\ d=4.5m \end{gathered}`

That is the depth of the pool.