ANSWER
3200 m²
Step-by-step explanation
Peter wants to build a fence around a rectangular field, except for one side because the river is there,
So, the total perimeter of the fence is,
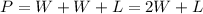
And this is equal to 160 m. Solving for L,
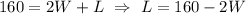
The area of this field is,
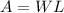
Replace L with the expression we found from the perimeter,
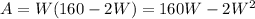
The area is given by a quadratic function whose leading coefficient is negative, which means that the graph is a downward parabola and, therefore, the vertex is the maximum value of the area.
The x-coordinate of the vertex is given by,
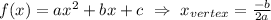
In this case, x is W, a = -2, and b = 160, so the width of the field for the maximum area is,
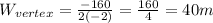
And the length when W = 40 is,
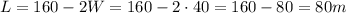
And the area is,
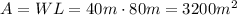
Hence, the largest area of Peter's farm that can be fenced is 3200 square meters.