Question

Find the value of X. If ur answer is not an integer

Answer 1

Answer: x = (5√2)/2

The last option

Step-by-step explanation:

The given triangle is a right triangle. Taking angle 45 as the reference angle,

hypotenuse = 5

opposite side = x

We would find x by applying the sine trigonometric ratio which is expressed as

sin θ = opposite side/hypotenuse

By substituting the given values into the equation,

sin45 = x/5

Recall,

`sin45\text{ = }(√(2))/(2)`

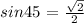
Thus,

`\begin{gathered} (√(2))/(2)\text{ = }(x)/(5) \\ By\text{ crossmultiplying,} \\ x\text{ = }(5√(2))/(2) \end{gathered}`

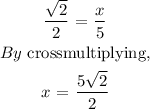
x = (5√2)/2

The last option