Given an expression:
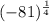
We have to simplify the expression, if it does not result in a real number then the answer is NONE.
Let:
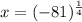
Then,
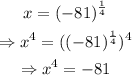
There is no real number whose power 4 is a negative number.
Thus, the answer is not a real number. The answer is NONE.