15. In circle A, SQ = 12 and AT = 8. Find AR.AR =AR

Question

asked Apr 10, 2023 35.1k views

1 Answer

Taufik Nurrohman · Answer 1 · 2023-04-16T01:44:30+0000

We have to find the length of AR.

It will be the same as the length of AS, as they are both radius of the circle:

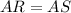
AS is the hypotenuse of a right triangle with legs AT and TS.

Also, TS has half the length of SQ, so we have:

$TS=(1)/(2)SQ=(1)/(2)\cdot12=6$

We then can calculate AS as:

$\begin{gathered} AS^2=TS^2+AT^2 \\ AS^2=6^2+8^2 \\ AS^2=36+64 \\ AS^2=100 \\ AS=\sqrt[]{100} \\ AS=10 \\ \Rightarrow AR=10 \end{gathered}$

Answer: AR = 10