Solution:
Scott paid;
$13.24 for 3.41-pound bag of shrimp
This means,
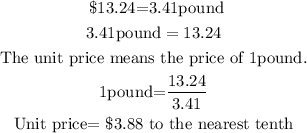
$18.99 for 4.96-pound bag of shrimp
This means,
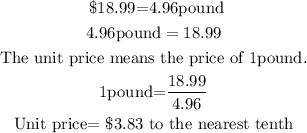
Therefore, the bag that is a better buy based on the unit price is the 4.96-pound because of the unit price which is lesser than the unit price for the 3.41-pound bag.
Thus, the 4.96-pound is a better buy.