Question

The largest angle of a triangle measures 9degrees less than 5 times the measure of the smallest angle. The middle angle measures three times that of the smallest angle. Find the measures of the three angles.

Answer 1

Let the smallest angle be represented as

`=x`

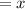
Step 1: The largest angle of a triangle(let the largest angle =z) measures 9degrees less than 5 times the measure of the smallest angle, this statement is represented as

`\begin{gathered} 5\text{ times the smallest angle gives} \\ =5* x \\ =5x \\ 9\text{ degr}ees\text{ less will give the largest angle to be} \\ \text{largest angle =5x-}9 \\ z=5x-9 \end{gathered}`

Step 2: let's calculate the middle angle (let the middle angle =y)

The middle angle measures three times that of the smallest angle, which means that

`\begin{gathered} y=3* x \\ \text{middle angle =y= 3x} \\ y=3x \end{gathered}`

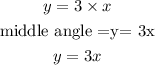
Recall that the total angles in a triangle give

`=180^0`

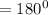
Therefore,

`\begin{gathered} \text{largest angle + middle angle + smallest angle =180}^0 \\ z+y+x=180^0 \end{gathered}`

Substituting we will have

`\begin{gathered} 5x-9+3x+x=180^0 \\ \text{collect the sinmilar terms we will have} \\ 5x+3x+x=180^0+9^0 \\ 9x=189^0 \\ \text{divide both sides by 9} \\ (9x)/(9)=(189^0)/(9) \\ x=21^0 \end{gathered}`

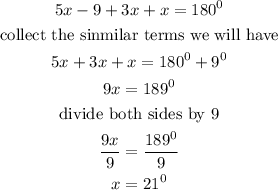
Hence,

the smallest angle is = 21 degrees

`\begin{gathered} \text{The largest angle =5x-9} \\ =5*21^0-9 \\ =105^0-9 \\ =96^0 \end{gathered}`

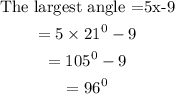
Hence,

The largest angle = 96 degrees

`\begin{gathered} \text{The middle angle=}3x \\ =3*21^0 \\ =63^0 \end{gathered}`

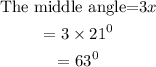
Hence,

The middle angle = 63 degrees