Given that Angelo's kayak travels 10km/h in still water, and the river's current flows at a rate of 4km/h.
Travelling downstream means Angelo is travelling with the current, that is the current of the water will add to Angelo's speed.
Their combined speed will be;

To travel 35 km downstream;
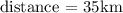
Recall that;

substituting the given values;
![\begin{gathered} \text{time = }\frac{35\operatorname{km}}{14\text{ km/h}} \\ \text{time =2.5 hours} \end{gathered}]()
Therefore, it'll take 2.5 hours
![undefined]()