Given:
The ratio of the diagonals of the squares ABCD and DEFG is:
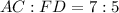
Required-the value of CE.
Step-by-step explanation:
Given that the ratio of the diagonals of the squares ABCD and DEFG is:
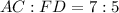
So, the sides will be in the same ratio.
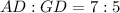
Let the sides of the two triangles ABCD and DEFG be 7x and 5x.
Given that
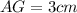
So, we can write AG as:
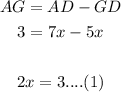
Now, we have to find CE, so we can write CE as:
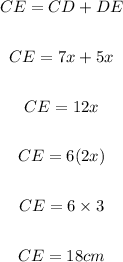
Final answer: The value of CE is 18 cm.