Given that there is a cart of mass, m = 0.12 kg moving with initial speed of, u1 = 0.45 m/s and it collides with another cart of mass, m = 0.12 kg with initial speed, u2 = 0 m/s
We have to find the initial and final kinetic energy.
(a) Initial kinetic energy,
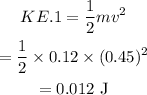
According to the conservation of linear momentum,
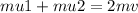
Here, v is the final speed.
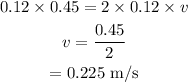
Here, the final speed is 0.225 m/s.
(b) The formula to find kinetic energy is
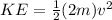
Substituting the values, we get
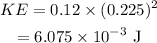
Hence the kinetic energy is 6.075 x 10^(-3) J.