Question

Graph each pair of lines and use their slopes to determineif they are parallel, perpendicular, or neither.EF and GH for E(-2, 3), F(6, 1), G(6,4), and H(2,5)JK and LM for J(4,3), K(5, -1), L(-2, 4), and M(3,-5)NP and QR for N(5, -3), P(0, 4), Q(-3, -2), and R(4, 3)ST and VW for S(0, 3), T(0, 7), V(2, 3), and W(5, 3)

Answer 1

To find the slope of a line that passes through two points, we can use the following formula:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope and} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points which the line passes} \end{gathered}`

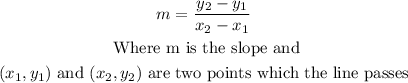
Then, we have:

First pair of lines

Line EF

`\begin{gathered} (x_1,y_1)=E\mleft(-2,3\mright) \\ (x_2,y_2)=F\mleft(6,1\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(1-3)/(6-(-2)) \\ m=(1-3)/(6+2) \\ m=(-2)/(8) \\ m=(2\cdot-1)/(2\cdot4) \\ m=-(1)/(4) \end{gathered}`

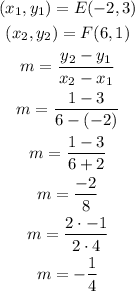
Line GH

`\begin{gathered} (x_1,y_1)=G\mleft(6,4\mright) \\ (x_2,y_2)=H\mleft(2,5\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(5-4)/(2-6) \\ m=(1)/(-4) \\ m=-(1)/(4) \end{gathered}`

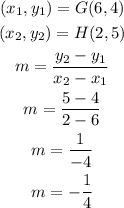
Now, when graphing the two lines, we have:

If two lines have equal slopes, then the lines are parallel. As we can see, their slopes are equal, therefore the lines EF and GH are parallel.

Second pair of lines

Line JK

`\begin{gathered} (x_1,y_1)=J\mleft(4,3\mright) \\ (x_2,y_2)=K\mleft(5,-1\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(-1-3)/(5-4) \\ m=-(4)/(1) \\ m=-4 \end{gathered}`

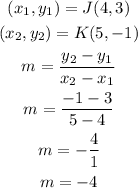
Line LM

`\begin{gathered} (x_1,y_1)=L\mleft(-2,4\mright) \\ (x_2,y_2)=M\mleft(3,-5\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(-5-4)/(3-(-2)) \\ m=(-9)/(3+2) \\ m=(-9)/(5) \end{gathered}`

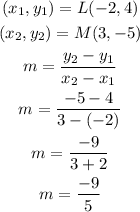
Now, when graphing the two lines, we have:

As we can see, the slopes of these lines are different, so they are not parallel. Let us see if their respective slopes have the relationship shown below:

`\begin{gathered} m_1=-4 \\ m_2=-(9)/(5) \\ m_1=-(1)/(m_2) \\ -4\\e-(1)/(-(9)/(5)) \\ -4\\e-((1)/(1))/((-9)/(5)) \\ -4\\e-(1\cdot5)/(1\cdot-9) \\ -4\\e-(5)/(-9) \\ -4\\e(5)/(9) \end{gathered}`

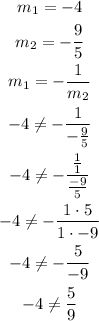
Since their respective slopes do not have the relationship shown below, then the lines are not perpendicular.

Third pair of lines

Line NP

`\begin{gathered} (x_1,y_1)=N\mleft(5,-3\mright) \\ (x_2,y_2)=P\mleft(0,4\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(4-(-3))/(0-5) \\ m=(4+3)/(-5) \\ m=-(7)/(5) \end{gathered}`

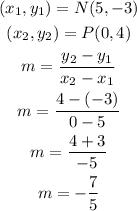
Line QR

`\begin{gathered} (x_1,y_1)=Q\mleft(-3,-2\mright) \\ (x_2,y_2)=R\mleft(4,3\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(3-(-2))/(4-(-3)) \\ m=(3+2)/(4+3) \\ m=(5)/(7) \end{gathered}`

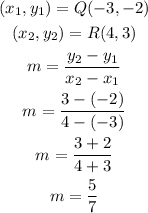
Now, when graphing the two lines, we have:

Two lines are perpendicular if their slopes have the following relationship:

`\begin{gathered} m_1=-(1)/(m_2) \\ \text{ Where }m_1\text{ is the slope of the first line and }m_2\text{ is the slope of the second line} \end{gathered}`

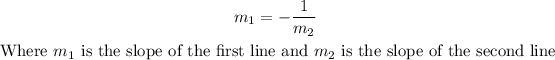
In this case, we have:

`\begin{gathered} m_1=-(7)/(5) \\ m_2=(5)/(7) \\ -(7)/(5)_{}=-\frac{1}{(5)/(7)_{}} \\ -(7)/(5)_{}=-\frac{(1)/(1)}{(5)/(7)_{}} \\ -(7)/(5)_{}=-(1\cdot7)/(1\cdot5)_{} \\ -(7)/(5)_{}=-(7)/(5)_{} \end{gathered}`

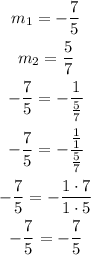
Since the slopes of the lines NP and QR satisfy the previous relationship, then this pair of lines are perpendicular.

Fourth pair of lines

Line ST

The line ST has an indefinite slope because it is not possible to divide by zero. Lines that have an indefinite slope are vertical.

Line VW

`\begin{gathered} (x_1,y_1)=V\mleft(2,3\mright) \\ (x_2,y_2)=W\mleft(5,3\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=\frac{3-3_{}}{5-2} \\ m=(0)/(3) \\ m=0 \end{gathered}`

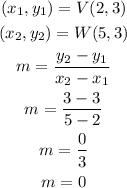
Line VW has a slope of 0. Lines that have a slope of 0 are horizontal.

Now, when graphing the two lines, we have:

As we can see in the graph, the ST and VW lines are perpendicular.