5. Let the following inequality:
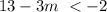
this is equivalent to:

this is equivalent to:
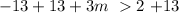
this is equivalent to:
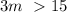
solve for m:
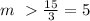
that is :
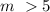
6. Because of the graphic (real line), we can conclude that the correct interval would be:
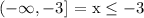
Then we have to find the inequalities that have this solution interval.
a) Let the inequality
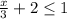
this is equivalent to:

this is equivalent to:
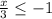
solve for x:
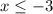
then. A) represent the graph.
b)Let the inequality
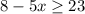
this is equivalent to:
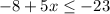
this is equivalent to:
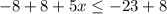
this is equivalent to:
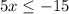
solve for x:
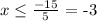
then the solution interval would be:
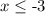
then. B) represent the graph.
c) Let the inequality:
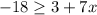
this is equivalent to:
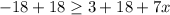
this is equivalent to:
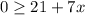
this is equivalent to:

solve for x:
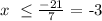
that is:
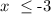
then. C) represent the graph.
d) Let the inequality:

this is equivalent to:
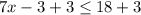
this is equivalent to:
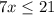
solve for x:
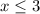
We can conclude that this interval does not represent the graph because:

Finally:
e) Let the inequality:
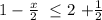
this is equivalent to:
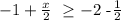
this is equivalent to

that is:
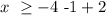
that is:

THEN WE CAN CONCLUDE THAT THE CORRECT ANSWER ARE:
A), B), C) AND E)