1 Answer

Ask a Question

Edharned · Answer 1 · 2023-12-14T16:40:12+0000

Answer:

(a) between 357 and 737

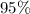
$95\text{\%}$

(b) above 642.

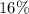
$16\text{\%}$

(c) below 357.

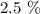
$2.5\text{ \%}$

(d) between 262 and 737.

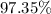
$97.35\text{\%}$

Step-by-step explanation:

Given that the GMAT scores are approximately normally distributed with a mean of 547 and a standard deviation of 95.

$\begin{gathered} \operatorname{mean}m=547 \\ \sigma=95 \end{gathered}$

To estimate the percentage of scores that were between the given interval let us use the normal distribution curve;

Solving for the percentage;

(a) between 357 and 737

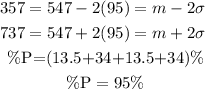
$\begin{gathered} 357=547-2(95)=m-2\sigma \\ 737=547+2(95)=m+2\sigma \\ \text{ \%P=(13.5+34+13.5+34)\%} \\ \text{ \%P}=95\text{\%} \end{gathered}$

(b) above 642.

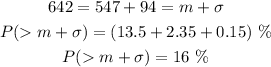
$\begin{gathered} 642=547+94=m+\sigma \\ P(>m+\sigma)=(13.5+2.35+0.15)\text{ \%} \\ P(>m+\sigma)=16\text{ \%} \end{gathered}$

(c) below 357.

$\begin{gathered} 357=m-2\sigma \\ P((d) between 262 and 737. %[tex]\begin{gathered} 262=547-3(95)=m-3\sigma \\ 737=m+2\sigma \\ P(262\text{ to 737)}=(2.35+13.5+34+34+13.5)\text{\%} \\ P=97.35\text{\%} \end{gathered}$

34. GMAT scores are approximately normally distributed with a mean of 547 and a standard-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions